Intro:
So - some context. I came to machine learning from a bioinformatics algorithms background and don’t have a ton of experience with the mechanics underlying the tools I use every day. However, I do understand how GPUs work, and how to write CUDA code to utilize the GPUs to do work, as I spent 99% of my dev work in my previous role writing HPC algorithms in CUDA / C++. Now, a lot of this is abstracted away from me by some amazing Python libraries like PyTorch, TensorFlow, and JAX so I still don’t really get to interact with the “meat” of what runs these amazing ML algorithms - and that is what I’m setting out to explore.
I’m going to do my best to make this content approachable for people without a math background, but it’s important to note that the very term “tensor” is a mathematical concept. Just hang in there with me.
Tensor Parallelism is at the heart of the applications we use for things like LLM inference, fine-tuning, model training, etc. - but what is Tensor Parallelism? Hell, what is a tensor? Why is this the construct we’ve used to describe the systems we are building? These are the questions I will dig into over this article. In subsequent articles, I will implement a naive TP in CUDA, followed by a more specific implementation of TP for MLP Layers, performing a NCCL all-reduce to converge results, implementing attention layers - and more depending on where the journey takes me. Many of these words and concepts may be unfamiliar to you - and that’s okay! They’re unfamiliar to me too. Given that, if you approach this as an expert, you may notice that I make some mistakes. That’s okay - and I’d be happy for you to correct me as I am learning along with many of you.
What exactly are Tensors?
Tensors as a mathematical construct have been around for quite some time - used to represent a set of numbers with some transformation properties.
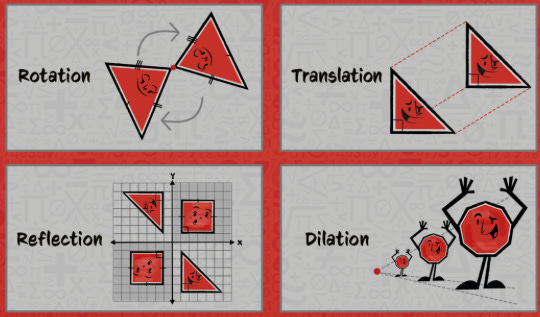
Transformation properties mean changing the position or appearance of an object by moving it, flipping it, or spinning it, while still keeping some parts of the object the same, like its angles or size depending on the transformation type. This image from Mathnasium helps:
Albert Einstein brought tensors into the spotlight by developing and formulating his theory of general relativity with tensor calculus.
Tensors generalize scalars, vectors, and matrices into higher-dimensional spaces:
scalar: quantities described by a magnitude (volume, density, speed, energy, mass, time, etc)
vector: quantities described by a magnitude and a direction (displacements, velocity, acceleration, force, etc)
matrix: a rectangular array of numbers - a vector could be a special type of matrix with one column or row, and a scalar can be seen as a 1x1 matrix with a single value.
# Tensors
scalar = [5] # 1x1 (1 row, 1 column)
vector = [ 1, 2, 3 ] # 1x3 (1 row, 3 columns)
matrix = [
[1, 2, 3],
[4, 5, 6],
] # 2x3 (2 rows, 3 columns)If we relate this back to our transformation definition, we can apply a “transpose” transformation, which simply flips rows and columns:
scalar = [5] # 1x1, the transpose is itself
vector = [ 1, 2, 3]^T = [[ 1 ] # (1x3) -> (3x1), row becomes column
[ 2 ]
[ 3 ]]
matrix = [ = [[1, 4], # (2x3) -> (3x2),
[1, 2, 3], [2, 5], # rows become columns
[4, 5, 6], [3, 6]]
]^TTo summarize, a tensor is basically an abstraction of these different numeric representations of objects. However, it’s important to note that this abstraction can be extended further. There is no reason that a tensor could not contain multiple matrices. Tensors, then, can extend beyond matrices to include higher-dimensional structures, making them fundamental in deep learning.
Ranks
A rank is a concept that refers to a tensor’s number of indices or dimensions. A rank-0 tensor is a scalar, a rank-1 tensor is a vector, a rank-2 tensor is a matrix, and higher-rank tensors have 3 or more dimensions. The rank of a tensor influences the transformations it can undergo, such as reshaping, transposition, translation, and contraction which are crucial when dealing with multi-dimensional data.
Scalar (Rank-0 Tensor): 1 (or 1 x 1 as a trivial case)
Vector (Rank-1 Tensor): M x 1 (column vector) or 1 x M (row vector)
Matrix (Rank-2 Tensor): M x N (M rows, N columns)
Rank-3 Tensor: K x M x N (K matrices of size M rows, N columns)
Why Tensors for Machine Learning?
Well, in ML we often explain a single object with several dimensions. For example, an image can be described by pixels containing an intensity, position, and color. If we wanted to represent this image in a 3D movie, we could scale the ranks of the image to accommodate more attributes to provide depth and relation to other pixels. This is where tensors come in handy - for every additional attribute we want to use to describe our object, we can add an additional rank to our tensor.
Considering the oh-so-popular Large Language Model (LLM) saga we’re in, we can consider a prompt we type to the model. Tokenization is the process of transforming a prompt (sequence of text) into a sequence of numbers. Consider the following example:
rank-0 tensor: “Hello” converted to a token → 7860 → (1x1 scalar)
rank-1 tensor: “Hello world!” converted into a sequence of tokens → [7860, 128]
shape = (sequence length) → (1xN vector)rank-2 tensor: Multiple prompts converted into a batch of token sequences: [[7860, 128], [5409, 289], [78, 212]]
shape = (batch size, sequence length) → (MxN matrix)rank-3 tensor: Multiple prompts converted into a batch of token sequences with embeddings - shape = (batch size, sequence length, embedding size) → (KxMxN tensor)
Because tensors give us such a convenient way to represent objects in numeric space, they are a great representation for multi-dimensional analysis.
Why GPUs for Tensors?
Now that we understand the structure of a tensor and how it can represent arbitrary attributes of a real world object using rank-N tensors, why are GPUs great for working with these constructs?
Unlike CPUs which have a small number of powerful cores optimized for sequential tasks, GPUs have thousands of smaller cores designed for parallel processing. Tensor operations (like matrix multiplication, dot products, or convolutions) involve many independent calculations that can be executed simultaneously across these thousands of GPU cores.
Additionally, these rank-N tensors can actually be segmented row-wise or column-wise such that we can distribute operations on parts of the tensor across many GPUs - finally arriving at our definition of tensor parallelism. We parallelize tensor operations across GPUs, and combine our results when we are done with independent calculations. And that’s it! That’s what I’ll be implementing in the weeks and months to come.
Final Remarks
Thanks for bearing with me as I ventured through an introduction to tensor parallelism. In the weeks to come, I’ll begin implementing tensor parallelism in CUDA, each week building on the next. All code for the implementations will exist in this repository under a directory called “tensor_parallelism” (which doesn’t exist at the time of writing this):
https://github.com/drkennetz/cuda_examples
So if you’d like to follow along, don’t forget to watch the repo!
Thanks for reading, and I hope you found this useful!

Genuinely looking forward for your content to understand the nitty gritty of the GPU